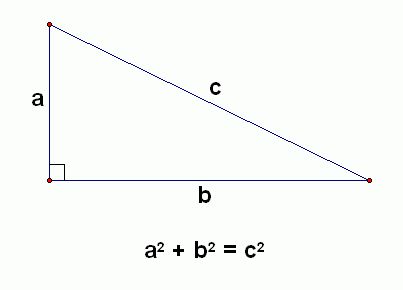ð Energy ð

Kinetic energy is a form of energy that represents the energy of motion. It is a scalar quantity, which means it has a magnitude but not a direction. It is, therefore, always positive. The kinetic energy, K (or sometimes E_k) is, therefore, defined as:

K = ½mv²

This quantity will always be a non-zero scalar quantity. If the object has a mass and is moving, it will always be positive. It will be zero in the case of a mass less object or an object at rest (zero velocity). The kinetic energy equation, therefore, gives us no information about the direction of the motion, only about the speed.

Potential energy is the stored energy of position. It can be thought of as energy that is “stored” by any physical system. It is called potential because, in its current form, it is not doing any work or causing any change in its surroundings. It does, however, have the potential to be converted to different forms of energy, such as kinetic. The standard unit for measuring such energy is the joule.

When an object is displaced from its original position and there is energy pulling it back to that position, potential energy tends to exist. A ball at the end of a spring, for example, has energy that will be converted to kinetic energy when allowed to return to its original position. A weight held above the ground will, when released, have potential energy as gravity pulls it back to its original position.

One of the major principles of potential energy is the law of conservation of energy, which states that energy can neither be created nor destroyed. The energy expended to lift an object or compress a spring does not simply disappear; it is “stored” as potential energy. It is then released as kinetic energy by a restoring force. The energy input equals the energy output; there is no gain or loss in overall energy. The potential energy, P (or sometimes E_P) is, therefore, defined as:

P = mgh

Д Adding Vector Components Д

 

Vectors	X	Y
A	-11.5	9.6
B	20	N/A
C	N/A	-13

1. Set your Positive Axes.

2. Break all vector down to two components (x and y). To help you keep your thoughts organized, use a graph as shown above.

3. Solve for ∑x and ∑y using the Pythagorean and the trigonometry equations.  

Vector A: 

X = Sin50° x 15km

    = 11.5km

Y= Cos50° x 15km

   = 9.6km

4. Use the Pythagorean to add the two sums of components(∑x and ∑y).

Total

8.5

-3.4

h²=a²+b²

h²=8.5²+3.4²

h²=83.81

h=9km 

5. Use trigonometry to solve for the angle

tanӨ= opp/adj

 = x/y  

      =8.5/3.4

=68°

6. Write your final results.

9 km [S68°E]

Ж Deriving Eq 4 from a Velocity-time Graph Ж

Ψ Deriving Eq 3 from a Velocity-Time Graph Ψ

§ Translation of Motion Time Graph §

Slope

Area

☼ Right Hand Rules ☼

   The Right Hand Rules were created by scientists to help us predict how magnetic forces act. They are called the Right Hand Rules because they involve using your right hand.



Right Hand Rule #1: for conventional current flow. Grasp the conductor with the thumb of the right hand pointing in the direction of conventional, or positive (+),  current flow. The curved fingers point in the direction of the magnetic field around the conductor.



Right Hand Rule #2: for conventional current flow. Grasp the coiled conductor with the right hand such that the curved fingers point in the direction of conventional, o positive (+), current flow. The thumb points in the direction of the magnetic field within the coil. Outside the coil, the thumb represents the north (N) end of the electromagnet produced by the coil.

Right Hand Rule #3: for conventional current flow: The motor principle. open the right hand so that the fingers point in the direction of the magnetic field (from north to south). Rotate the hand so that the thumb points in the direction of conventional (+) current flow. The orientation of the palm indicates the direction of the force produced.

♥ Magnetism and Electromagnetism ♥

17.1 The Magnetic Force -- Another Force at a Distance

      A magnetic field is the distribution of a magnetic force in the region of a magnet. The same theory can be applied to magnets as well as electrostatic forces - With electronic fields, there are two different magnetic characteristics, labeled north and south, that are responsible for magnetic forces. 

THE LAW OF MAGNETIC FORCE : Similar magnetic poles, north and north or south and south, repel one another with a force at a distance. Dissimilar poles, north and south, attract one another with a force at a distance. 

    To map a magnetic field you use a test compass, instead of the test charge we used is electrostatics. 
   The Earth itself acts as a giant permanent magnet, producing its own magnetic field. it is suggested that this magnetic field is produced because of the flow of hot liquid metals inside the Earth. Magnets are also known to attract other materials such as iron, nickel, and cobalt, or mixtures of these three. They are called the ferromagnetic metals. 
DOMAIN THEORY: All large magnets are made up of many smaller and rotatable magnets, called dipoles, which can interact with other dipoles close by. if dipoles line up, then a small magnetic domain is produced. 
17.2 Electromagnets
OESTED'S PRINCIPLE : Charge moving through a conductor produces a circular magnetic field around the conductor. 
    To help us predict how magnetic forces act, scientists have developed several hand signs  called right-hand rules because they involve using your right hand. 
↓  Predicts the direction of the magnetic field around a straight conductor. 
RIGHT-HAND RULE #1 for conventional current flow Gasp the conductor with the thumb of the right hand pointing in the direction of conventional, or positive, current low. The curved fingers point in the direction of the magnetic field around the conductor. 
↓  Predicts the relationship between the direction of convectional current flow in a coil and the direction of the magnetic field at the end of the electromagnet. 
RIGHT-HAND RULE #2 for convectional current flow Grasp the coiled conductor with the right hand such that curved fingers point in the direction of conventional, or positive, current flow. The thumb points in the direction of the magnetic field within the coil. Outside the coil, the thumb represents the north end of the electromagnet produced by the coil.